Назад

Это страница с нашими курсовиками по специальности 2203 за 4 курс графака в С++

здесь я напишу про свой курсовой проект

значит так постановка задачи: " В с++ под дос надо построить фрактальную кривую таким образом чтобы на отрезке прямой ставятся две точки и строится равностороний треугольник потом каждая сторона треугольника делиться пополам и строится такойже треугольник и так до бесконечности"

------ну сначало немного о самих фракталах и о кривой КОХ

Имеются различные определения понятия "фрактал", однако уже почти четверть века назад один из ведущих специалистов в этой области, бельгийский математик Бенуа Мандельброт (его именем назван один из самых знаменитых фрактальных объектов — множество Мандельброта, алгоритм построения изображения которого мы также рассмотрим), отмечал, что ни одно из определений не представляется удовлетворительным, ибо всегда находятся объекты, которые, по-видимому, имеют фрактальную природу, но не удовлетворяют данному определению. Понятие фрактала в чем-то схоже с понятием компьютерного вируса. И в том, и в другом случае не существует (на данный момент) строгого определения понятия, но есть некоторое характерное свойство (также плохо формализуемое), которое присуще всем объектам, которые принято относить к данному классу. Для компьютерных вирусов таким свойством является способность к самовоспроизведению, для  фракталов — самоподобие. Именно на это свойство, как на характерное для всех известных фракталов различной природы, указывал и Б.Мандельброт.

ТЕПЕРЬ РАСМОТРИМ ЧТО НАМ НАДО ПОСТРОИТЬ Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

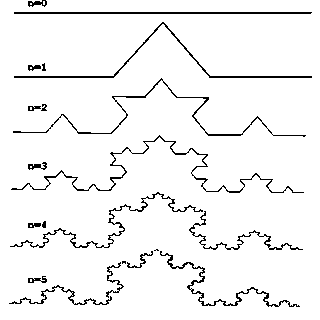
Рисунок 1 - Построение триадной кривой Кох.

Рассмотрим один из таких фрактальных объектов - триадную кривую Кох [3]. Построение кривой начинается с отрезка единичной длины (рис.1) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис.1 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным обьектом [3].

эту кривую будем делать с помощю так называймой "черепашей графикой"

Рассмотрим исполнителя (черепашку), который имеет память, организованную в виде стека (т.е. он может вспомнить лишь то, что запомнил в последний раз), и умеет "ползать по плоскости" и выполнять несколько простых команд (см. ниже).

Текущее состояние черепашки описывается набором из трех параметров (х, у, a):

   х, у — текущие' координаты черепашки;
   a — угол, определяющий направление, в котором черепашка ползет по команде "вперед".

Начальное состояние черепашки описывается набором из пяти параметров: (х₀, y₀, a₀, step_move, step_a). Здесь х₀, y₀, a₀ — начальные значения координат и угла, а
step_move — шаг (шаг определяет длину одного шага черепашки, который она делает по команде "вперед");
step_a — угол поворота (угол поворота определяет, на сколько поворачивается черепашка, иными словами, на сколько меняется угол а при выполнении команд "налево" и "направо").

Черепашка умеет выполнять следующие команды (каждая команда кодируется одним символом):

"F" — переместиться вперед (на step_move), в направлении а, оставив след (отрезок);
"+" — повернуться направо (по часовой стрелке) на угол step_a (при исполнении этой команды меняется только угол а);
"—" — повернуться налево (против часовой стрелки) на угол step_a (при исполнении этой команды также меняется только угол а);
" [" — запомнить (отложить в стек) текущее состояние (х, у, a);
" ] " — вспомнить (взять из стека и установить) последнее запомненное состояние***но это нам не понадобиться(это для более сложных фракталов )

Программой для черепашки является строка, в которой, кроме указанных символов, могут встречаться и любые другие. Черепашка просматривает строку-программу символ за символом. Команды она выполняет, а символы, не являющиеся командами, пропускает.

Рассмотрим два примера (мы будем приводить лишь строку-программу и угол поворота step_a, поскольку остальные параметры влияют на ориентацию и размер» но не на вид фрактальной кривой).

Строка-программа:

- - - -F [+] [-]F[-FFF] [+FFF]F[+F[+
][-]] [-F[+] [-]]F[-FFF] [+FFF]F[-F
FF] [+FFF]F[-FFF] [+FFF] F [+F [+]
[-]F[-FFF][+FFF]F[+F[+] [-] ] [-F
[l+] [-]]] [-F[+] [-]F[-FFF] [+FFF]
F[+F [+][-] ][-F [+][-]]]
Угол поворота: (360/14) градусов (мы привели его в таком виде, поскольку в программах используется не сам этот угол, а число, на которое делится 360, т.е. 14).

Строка-программа:

-----[++++-[+][-+[-]][-
FFF] [+FFF] F][---+-[+][-
 +[-]] [-FFF] [+FFF]F][-
FFF][+FFF]F[++++[-]][[-
--+[-]][+++][---][-
FFF] [+FFF] FFFF
Угол поворота: (360/20)

Разумеется, приведенные здесь строки-программы мы получали не "руками". Рассмотрим алгоритм получения этих строк, предложенный А.Линдермауером.

Пусть имеются некоторая строка, которую мы назовем аксиомой (ахioms), и набор строк, называемых правилами (rule₁, rule₂, ... rule_n). Аксиома может быть любой, а правила должны иметь вид символ —> строка. Приведем пример:

Аксиома: ----G
Правила: G->GFX [+G] [-G]
                 X->X[-FFF] [+FFF]FX

Сначала положим результирующую строку равной аксиоме. Станем просматривать ее слева направо. Если встречается символ, являющийся первым символом одного из правил, заменим его на строку из соответствующего правила.

Так, после первого шага из приведенной аксиомы и правил получается следующая строка: ----GFX [+G] [-G].

После второго шага: ----GFX[+G] [-G]FX[-FFF] [+FFF] FX [+GFX [+G] [-G] ] [-GFX[+G] [-G] ]

И, наконец, после третьего шага: -—GFX [+G] [-G]FX[-FFF] [+FFF]FX[+GFX[+G] [-G] ] [-GFX[+G] [-G]]FX[-FFF] [+FFF]FX[-FFF] [+FFF]FX[-FFF] [+FFF] FX [+GFX [+G] [-G]FX[-FF F] [+FFF] FX [+GFX [+G] [-G] ] [-GFX[+G] [-G] ] ] [-GFX[+G] [-G]FX[-FFF] [+FFF] FX [+GFX [+G] [-G] ] [-GFX[+G] [-G]]]

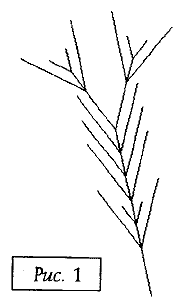
Если удалить из полученной строки все "незначащие" символы, то получится строка-программа, по которой был построен рис. 1.

Назад